Why Rasa uses Sparse Layers in Transformers

RandomlyConnectedDense Layers

Remark on nomenclature.

In Rasa 2.5 and earlier the RandomlyConnectedDense layers where called DenseWithSparseWeights, and instead of the connection_density parameter we had a weight_sparsity parameter.

In our transformer-based models (DIET and TED), we replace most Dense layers with our own RandomlyConnectedDense layers. The latter are identical to Dense layers, except that they connect only some of the inputs with any given output.

You can use the connection_density parameter to control how many inputs are connected to each output. If connection_density is 1.0, the RandomlyConnectedDense layers are identical to Dense layers. As you reduce the connection_density, fewer inputs are connected to any given output. During initialization the layer chooses randomly which connections are removed. But it guarantees that, even at connection_density = 0.0:

• every output is connected to at least one input, so the output is dense, and
• every input is connected to at least one output, so we don't ignore any of the inputs.

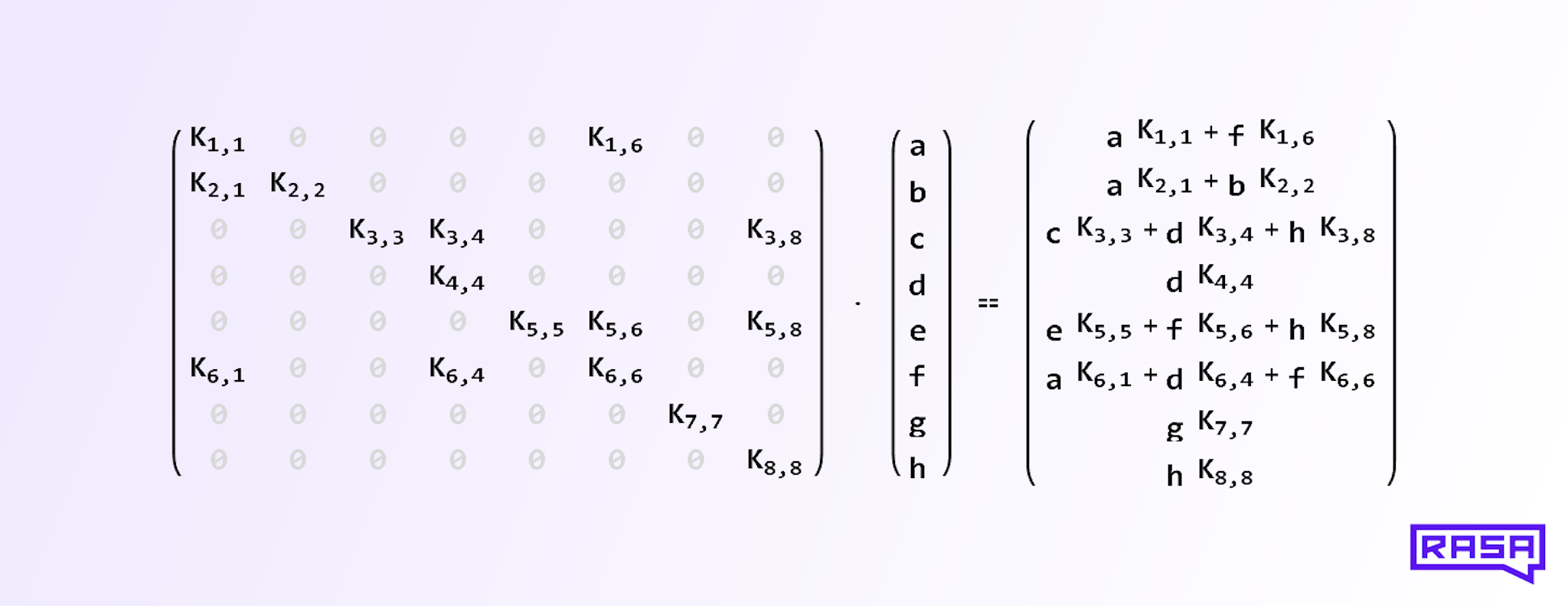
On the implementation level, we achieve this by setting a fraction of the kernel weights to zero. For example, a RandomlyConnectedDense layer with 8 inputs and 8 outputs, no bias, no activation function, and a connection_density of 0.25, might implement the following matrix multiplication of the kernel matrix with the input vector:

The 8x8 kernel matrix on the left contains 16 = 0.25 * 8^2 random entries. Each output on the right hand side therefore contains a linear combination of some of the input vector entries a, b, c, and so on. Which entries enter this linear combination is random, because we choose the position of the zeros in each row of the kernel matrix at random during initialization (except the diagonal, which guarantees that at least one input is connected to each output and vice versa).

Note, that this is different from weight pruning, which is done after training. It is also different from neural networks that learn a sparse topology during training. In our case the topology ("which inputs are connected to which outputs") is random and doesn't change during training.

Why do we do this, and why is this not detrimental to performance? Read on to find out.

Randomly Connected Layers in DIET

Rasa's Dual Intent and Entity Transformer (DIET) classifier is a transformer-based model. The transformer in DIET attends over tokens in a user utterance to help with intent classification and entity extraction. The following figure shows an overview of the most important aspects of a layer in DIET's transformer.

All of the W... layers inside the transformer that are usually Dense layers in other applications are RandomlyConnectedDense in Rasa. Specifically, the key, query, value, attention-output, and feed-forward layers in each transformer encoder layer, as well as the embedding layer just before the encoder, are RandomlyConnectedDense in Rasa.

By default, outputs of any RandomlyConnectedDense layer in DIET's transformer are only connected to 20% of the inputs, i.e. connection_density = 0.20 and we might call these layers sparse.

Why do we do this? Let's compare DIET's performance on intent classification with different densities and transformer sizes.

The figure above shows how the weighted average F1 test score for intent classification on the Sara dataset depends on the number of trainable weights in the sparse layers. The green graph corresponds to density = 1.0, i.e. all layers are Dense layers and we change the layer size to alter the number of trainable weights. We see that in this fully dense case, the performance first increases rapidly between 1,000 and 5,000 weights, and then stays nearly constant all the way up to 1,000,000 weights. Note, that the horizontal axis is scaled logarithmically.

Now consider the yellow, blue, and red graphs in the figure. Here we use sparse layers with densities of 20%, 5%, and 1%, respectively. We see that the lower the density, the fewer trainable weights are needed to reach the same level of performance. When we use only 1% of the connections (red graph), we need only 5,000 trainable weights to achieve the same level of performance as with 400,000 weights in a dense architecture!

This picture changes a bit for the entity extraction task on the same dataset, as we show in the figure below.

DIET reaches peak performance at about 100,000 trainable weights with 100% dense layers, which is on par with 20% dense layers with much fewer trainable weights (right end of yellow graph). But if we decrease the density to 1%, performance can drop significantly, even when we make layers very large (right end of the red graph). So we cannot reduce density arbitrarily, but it is still true that sparse layers (at 20% density) perform pretty much as well as dense layers with many more trainable weights.

Due to the way Tensorflow is implemented and hardware is built, the reduced number in trainable weights does not mean, unfortunately, that we can save time during training or inference by making layers less dense. It might be that convergence during training is more robust, but we are still investigating this hypothesis. For now, our primary reason to use sparse layers is Occam's Razor: When you have two models that do the same thing, but one of them has fewer parameters, then you should choose the latter.

Randomly Connected Layers in TED

Do our findings of the previous section also hold for other models? Let's have a look at our favorite machine learning model on the dialogue management side: the Transformer Embedding Dialogue (TED) policy. After each step in a conversation, TED decides what action Rasa should take next. We think of this as a classification problem: It should choose the right action (the class) for any given dialogue state (the input).

TED contains the same transformer component that we discussed in the DIET Section, and therefore TED also contains many RandomlyConnectedDense layers. We evaluate TED in the same way we evaluate DIET, but here we use the Conversational AI Workshop dataset, which contains more interesting stories.

The above figure shows that the dense architecture (green graph) reaches peak performance at about 21,000 trainable weights. But as in DIET, we achieve the same performance with a 20% dense layer that contains only 5,000 trainable weights in RandomlyConnectedDense layers. If we reduce the density further, the limiting performance declines, so we shouldn't go much below 20% density in real applications.

Why does this Work?

Why do models not immediately lose performance as we reduce the connection density? In particular, why is a 20% dense transformer as good as a fully dense transformer? And why does it not matter which inputs we connect to any given output?

To understand this, let's first realize that much of the art of engineering neural networks lies in figuring out what not to connect. In principle, an infinite fully connected neural network can learn anything. But it is neither possible to implement, nor would it be efficient. So we need to impose some structure on the network (throw away some connections) such that it still learns what it needs to learn. A common technique is to prune weights away after training of a dense network. And in image processing, it is common to throw away a lot of connections by using convolutional layers instead of dense layers. We can guess beforehand that this particular structure works, because neighboring pixels in an image are more related to each other than pixels that are far apart.

In contrast to image processing, the neighboring dimensions ("pixels") of a natural language embedding have no guaranteed relation to each other (unless we use semantic map embeddings). But it makes sense that we can still drop most of the connections throughout training, like in a convolutional layer, since pruning works in language models.

So we can drop connections, but why can we choose randomly which ones to drop? This is because we always have at least one dense layer before all the sparse architecture and a single dense layer can learn to permute the inputs! So during training, the first dense layer learns to feed just the right information to the remaining sparse layers. And apparently this is enough for the models to learn as if they were fully dense all the way.